Uniform star polyhedron/Uniform polyhedra by Wythoff construction

According to (Coxeter, "Uniform polyhedra", 1954), there are 4 spherical triangles with angles π/p, π/q, π/r, where (r q p) are integers:

These are called Mobius triangles.

In addition Schwarz triangles consider (p q r) which are rational numbers. Each of these can be classified in one of the 4 sets above.

Right triangle generators

Operation	Parent	Truncated	Rectified	Truncated dual	Dual	Cantellated	Omnitruncated	Snub
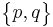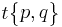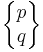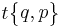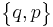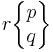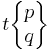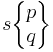(Extended-1) Schläfli symbols	$\begin{Bmatrix} p , q \end{Bmatrix}$	$t\begin{Bmatrix} p , q \end{Bmatrix}$	$\begin{Bmatrix} p \\ q \end{Bmatrix}$	$t\begin{Bmatrix} q , p \end{Bmatrix}$	$\begin{Bmatrix} q , p \end{Bmatrix}$	$r\begin{Bmatrix} p \\ q \end{Bmatrix}$	$t\begin{Bmatrix} p \\ q \end{Bmatrix}$	$s\begin{Bmatrix} p \\ q \end{Bmatrix}$
Wythoff Symbol p-q-2	q \| 2 p	2 q \| p	2 \| p q	2 p \| q	p \| 2 q	p q \| 2	2 p q \|	\| 2 p q
Vertex Figure	(p^q)	(q.2p.2p)	(p.q)²	(p. 2q.2q)	(q^p)	(p. 4.q.4)	(4.2p.2q)	(3.3.p. 3.q)
Dihedral symmetry
(2 2 2)
(3 2 2)
(4 2 2)
(5 2 2)
(5/2 2 2)
(5/3 2 2)
Tetrahedral symmetry
(3 3 2)	U1	U2	<U5>	U2	U1	<U7>	<U8>	<U22>
(3 3/2 2)	--	--	--	--	--	U04	--	--
Octahedral symmetry
(4 3 2)	U6	U9	U7	U8	U5	U10	U11	U12
(4 3/2 2)	--	--	--	--	--	U17	U18	--
(4/3 3 2)	--	--	--	U19	--	--	U20	--
(4/3 3/2 2)	--	--	--	--	--	--	U21	--
Icosahedral symmetry
(5 3 2)	U23	U26	U24	U25	U22	U27	U28	U29
(5 5/2 2)	U34	U37	U36	--	U35	U38	U39	U40
(5/2 3 2)	U52	U55	U54	--	U53	--	U56	U57
(5 5/3 2)	--	--	--	U58	--	--	U59	U60
(5/3 3 2)	--	U66	--	--	--	U67	U68	U69
(5/3 3/2 2)	--	--	--	--	--	--	U73	U74